论文认为:组合泛化(combinatorial generalization)是AI中最首要的任务,要达到这个目的,结构化表征(structured representations)和计算能力(computations)很关键。如生物学中,将先天基因和后天孕育结合在一起,因此我们必须摒弃在”手动设计结构(hand-engineering)“和”端到端(end-to-end)”二选一的错误做法,而是把两者结合起来:深度学习+基于结构的方法:图网络。
研究问题
要探索的是:如何在深度学习结构中学习实体(entities),关系(relations),规则(rules)并组合起来,然后在其结构中实现关系归纳偏置(relational inductive biases)?
对此,本文提出了一种可在AI中应用的新模块,即图网络,图网络通过提供一个接口用来操作结构化知识并处理结构上的行为。那么图网络如何实现关系推理(relational reasoning)和组合泛化(combinatorial generalization)呢?
一种关键的人类的智能能力——以有限表示无穷 (A key signature of human intelligence is the ability to make “in finite use of fi nite means”)。即用一些集合的元素(如句子,单词)进行无限的组合(组成句子,文章)。这也反映出了组合泛化原则:从已有的模块进行组合,来达到推理,预测等功能。
人类组合泛化能力依赖于我们对结构化表示和关系推理的认知(Humans’ capacity for combinatorial generalization depends critically on our cognitive mechanisms for representing structure and reasoning about relations.)。人类使用分级制来提取行为和表示的差别和共性,同时面对新颖的问题,会采用相似技能与常规经验相组合(composing familiar skills and routines)来解决。即:我们通过对齐两个域之间的关系结构,并根据其中一个域来对另一个域相对应的知识得出一个推论或类比。
我们在学习的时候(接受一个正确实例的时候), 可以做两个事情
- 将新的知识放入已有的结构化知识框架.
- 调整框架去适应新的知识.
对比过去的AI算法,往往都陷入“端到端”的设计哲学中,并强调最小化先验表征和计算假设,并避免明确的结构和手工设计结构。正是由于深度学习刻意避开了组合性和明确的结构方法,而面对像复杂语言、场景理解、结构化数据推理、基础训练上的迁移学习和少量经验学习这些需要组合泛化功能实现的任务,深度学习在这些任务上就难以实现了。
正如生物学里先天因素和后天因素是共同发挥作用的,本文认为“人工构造”(hand-engineering)和“端到端”学习也不是只能从中选择其一,本文主张结合两者的优点,从它们的互补优势中受益。
整篇文章都是从关系归纳偏置(relational inductive biases)的视角来研究各种深度学习方法,表明现有的方法往往带有关系假设,这些假设并不总是显式的或立即可见的。然后,文章提出了一个基于实体和关系的推理的通用框架——称之为图网络——用于统一和扩展现有的对图进行操作的方法,并描述了使用图网络作为构建块构建强大架构的关键设计原则。
关系归纳偏置(Relational inductive biases)
关系推理(relational reasoning):

- 实体(entitiy): 具有属性的元素,比如具有大小和质量的物体。
- 关系(relation): 实体之间的属性。两个物体之间的关系,比如具有相同的尺寸,A比B更重等。在这里,我们关注实体之间的配对关系。
- 规则(rule): 将实体和关系映射到新的实体和关系的函数。
图模型能取得成功是因为捕获到了真实世界生成过程的稀疏结构,并且支持能够进行推理和学习的算法。
归纳偏置(Inductive biases):
我们把在学习过程中,实体之间关系和相互作用施加约束叫做归纳偏置。

学习过程涉及到寻找一个解空间中的解,归纳偏置(inductive biases)允许一个学习算法优先选择一个解决方案或者解释方案(solution or interpretation)。归纳偏置经常会以提高灵活性来提高样本复杂性,并可由偏差-方差来权衡理解。
我们利用机器学习算法要做的是, 利用一个学习器, 通过学习样本使得学习器对于任意输入(可以不包含在训练数据中)可以产生正确的预测. 那么, 这个假设就决定了在面对未知数据下如何去作出判断. 例如, 在线性回归中, 作出的假设(归纳偏置)是, 输出与输入是线性的。
归纳偏置表还表现在:
- 最大边界:当要在两个类别间画一道分界线时,试图去最大化边界的宽度。这是用于支持向量机的偏置。这个假设是不同的类别是由宽界线来区分。
- 最小描述长度(Minimum description length):当构成一个假设时,试图去最小化其假设的描述长度。假设越简单,越可能为真的。见奥卡姆剃刀。
- 最少特征数(Minimum features):除非有充分的证据显示一个特征是有效用的,否则它应当被删除。这是特征选择(feature selection)算法背后所使用的假设。
- 最近邻:假设在特征空间(feature space)中一小区域内大部分的样本是同属一类。给一个未知类别的样本,猜测它与它最紧接的大部分邻居是同属一类。这是用于最近邻居法的偏置。这个假设是相近的样本应倾向同属于一类别。
需要注意的是,这些假设不需要是明确的,它们反映了模型或算法如何与现实世界交互。
关系归纳偏置
除此之外, 还有还有很多 no-relational inductive biase.
- activation non-linearities
- weight decay,
- dropout ,
- batch and layer normalization ,
- data augmentation
这些称为非关系归纳偏置, 与上面的关系归纳偏置进行对比, 我们就可以大概知道:
关系归纳偏置 是 应用了关系推理的归纳偏置. 是具有生成能力的.
Rel Inductive bias 推广到深度模型
深度学习中的各种模型其实就可以看作是由不同的初级building block组成的复杂的深层的层级结构或者图结构.
初级building block包括, “fully connected” , “convolutional layers”等等等等很多.
复杂的结构, 例如 MLP就是由多个 “fully connected” 组成的. 这个时候, “MLP” 也可以作为一个block.
而CNNs就是由 “convolutional layers” 和 “MLP” 组成的一个新的block.
最重要的是, 不同的block都包含着不同的 “relational inductive biase”, 也就是不同的设计指导思想.
下图是几个例子:

每个深度模型的entities, relations 和 rules都是不一样的, 为了更好的理解他们, 这里定义了几个术语.
- arguments : 是 rule functions的输入, 就是entities和relations
- reused, shared : 指的是 rule functions 是否被reused或者shared(也就是说不同relation(连线)之间是否使用相同的rules(激活函数,不同权重算不同函数)).
- interactions, isolation : 得出的结果是全部entities之间协作的结果的话就是interactions, 否则就是isolation.

Fully connected
- entities : 网络中的 units
- relations : all-to-all
- rules : 由 weights and biase 指定
- rules 的输入参数是 the full input signall, 而且 no reuse and no isolation of information.
- 关系归纳偏置 : very weak, 每个输入 units 都决定了输出的 units。
Convolutional layers
- entities : 还是独立的unit
- relations : 是稀疏的, 不再是全部连接.
- 关系归纳偏置 : locality and translation invariance
- locality : 意思是空间相近的实体有联系远的没有.
- translation invariance : 局部单元对于rules(卷积子)的复用,Spatial translation(平移不变性)
- 远距离单元之间是isolated 的
Recurrent layers
- rule : 接受 a step’s inputs 和 hidden state 作为arguments.
- reused : The rule is reused over each step
- 关系归纳偏置 : temporal invariance 全部是 Interaction.
Computations over sets and graphs
举了一个例子:
预测由 n 个行星组成的太阳系质心,其中的属性(例如,质量,位置,速度等)由 {x1, x2, …, xn}表示。对于这样的计算,行星的顺序并不重要,可以仅用汇总的平均质量来描述这个状态。然而,如果我们使用一个MLP来完成这个任务,学习某个特定输入(x1, x2, …, xn)的预测不一定会转化为在不同的排序下对同一个输入进行预测(xn, x1, …, x2)。既然有n!这种可能的排列,在最坏的情况下,MLP可以将每个排序视为不同,因此需要指数数量的输入/输出训练示例来学习近似函数。
当然,在许多问题中,置换不变并不是唯一重要的基本结构形式。例如,一个集合中的每个对象都可能受到集合中其他对象的成对交互的影响。在我们的行星场景中,现在考虑预测每个行星在一段△t时间间隔后的位置。在这种情况下,使用汇总的平均质量是不够的,因为每个行星的运动取决于其他行星对其施加的力量。相反,我们可以计算每个物体的状态 $x_i^{‘} = f(x_i,\sum_j g(x_i,x_j))$,其中 g函数计算第 j 个行星对第 i 个行星上产生的作用力,f 函数的输入是自身的重力和外力。(我们可以将相同的分析扩展到更加纠缠的结构,这些结构依赖于三元组之间的关系(即g (xi, xj, xk)),四元组等等。我们注意到,如果我们限制这些函数只对空间上接近的xi子集进行操作,那么我们会以类似于CNN的方式结束。在最纠结的意义上,在存在单个关系函数g (x1, …, xn)的情况下,我们以类似完全连接层的结构结束。)
上面的太阳系例子说明了两个关系结构:一种是不存在关系,另一种是包含所有配对关系。许多现实世界的系统属于这两个极端之间,比如,一些实体拥有关系而另一些实体没有关系。在我们的太阳系的例子中,如果系统由行星和它们的卫星组成,那么可以忽略其他行星和当前卫星之间的相互作用力。实际上,这意味着只计算一些对象之间的相互作用。
Graph Networks Block
图网络模型遍布监督学习,半监督学习,无监督学习,强化学习等领域。并能在视觉理解,few-shot learing ,动态物理结构(the dynamics of physical systems),多代理系统(multi-agent systems),知识图谱推理,预测化学分子和图像分割
接下来就是本文提出的 ‘graph network framwork’,使用图结构进行表征,在此基础上定义一类用来进行关系推理的函数。该 GN 框架泛化并扩展了多种图神经网络。MPNN,统一了不同种图网络和卷积云网络算法,NLNN则统一了多种“self-attention”算法。
注:图网络并不是只可以在神经网络上使用。
功能:
从一些基本的 building blocks 去构建复杂的结构
组成:
- GN框架的基本单元是 GN block.
- 输入是graph. (表现在网络中就是unit)
- 输出是graph
- 执行的是基于结构的计算
- graph 的 node 是实体(entities), edges 是 关系(relations)
图网络的设计理念:
灵活表示(Flexible representations)
可控内部结构 (Configurable within-block structure)
可组合多块体系结构(Composable multi-block architectures)
graph 的定义
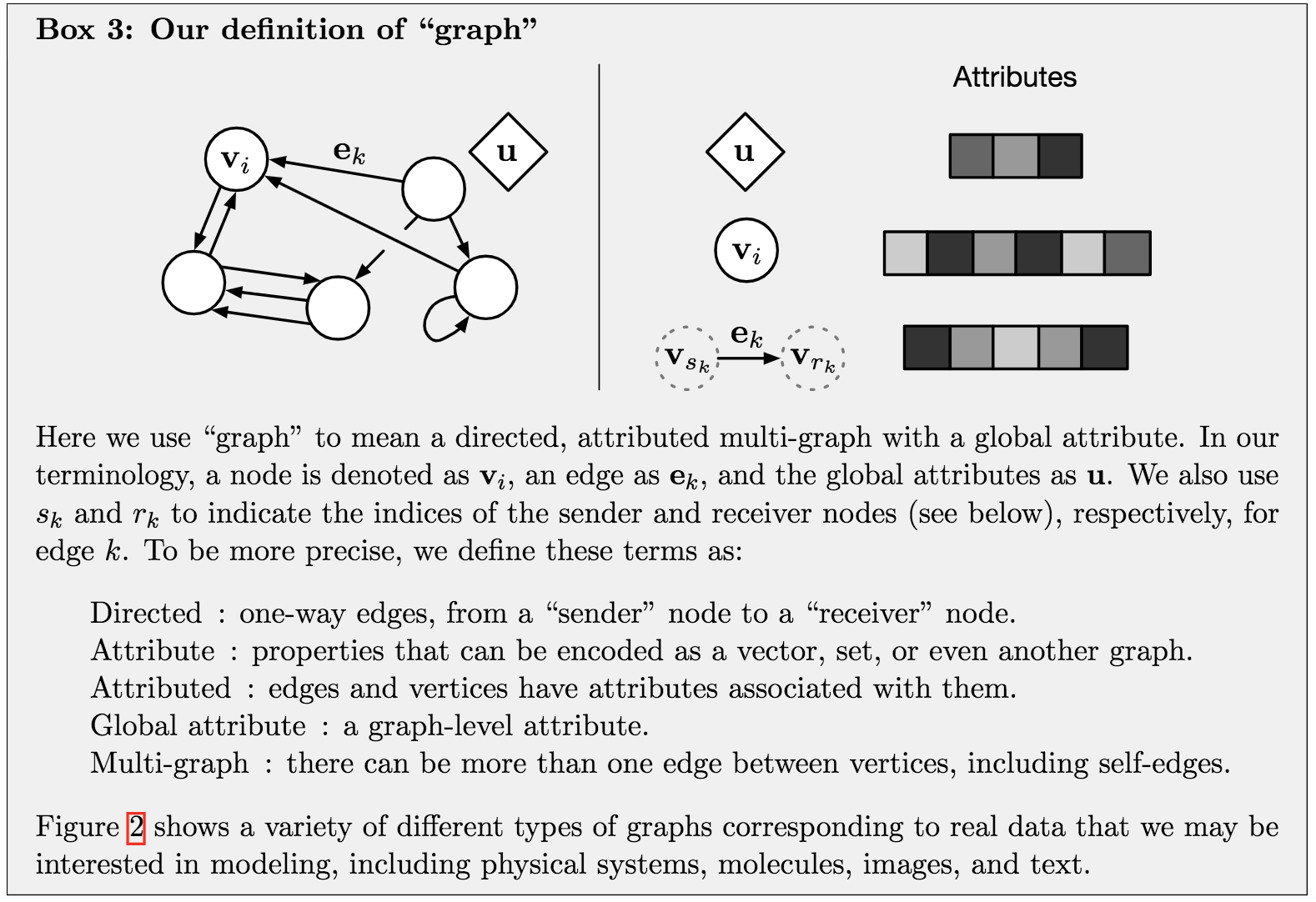
实体被定义为图的节点,关系为边。
图被定义为一个三元组,$G =(u,V,E)$
$node \; v_i$ : 拥有属性 attribute, 抽象含义是一个node, 具体值是 attribute $v_i$ 。
$V = { v}_{i =1: N_v} $, 是所有nodes的集合。$edge\; e_k$ : 拥有属性, 抽象含义是一个 edge, 具体值是 attribute $e_k$。
$E = { ( e_k ,r_k ,s_k ) }_{k =1: N_e} $, 是所有edges的集合。$global\; attributes\; u$: 图的全局属性。
上面是三个基本组成元素.
- “sender” node $s_k$ : edge $e_k$ 的发射端 node
- “receiver” node $r_k$ : edge $e_k$ 的接受端 node
Internal structure of a GN block
一个GN模块包括三个更新函数 $\phi$ 和三个聚合函数 $\rho$。

GN模块的计算步骤如下图:

注意:这三个基本组成元素的更新顺序可以被人为定义。
对每个边的状态进行的更新:
$$e_k^{‘} = \phi^e(e_k,v_{r_k},v_{s_k},u)$$
蓝色为输出, 黑色为输入

对每个点的状态进行的更新:
$$v_i^{‘} = \phi^v(\bar{e_i}^{‘},v_{i},u)$$
其中,$\bar{e_i}^{‘} = \rho^{e \rightarrow v}(E_i^{‘})$
$\rho$ 是个聚合函数, 其接受参数为一个边的集合. 然后利用集合中所有边的信息去调整一个node的状态.
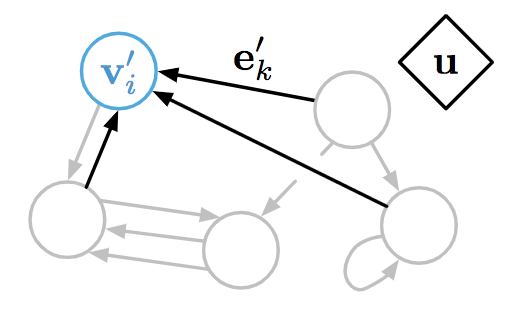
对全局状态进行跟新:
$$u^{‘} = \phi^u(\bar{e}^{‘},\bar{v}^{‘},u)$$
其中包含两个聚合函数:
$\bar{e}^{‘} = \rho^{e \rightarrow u}(E_i)$
$\bar{v}^{‘} = \rho^{v \rightarrow u}(V_i)$
第一个, 其接受参数为一个边的集合. 然后利用集合中所有边的信息去调整全局状态。
第二个, 其接受参数为一个点的集合. 然后利用集合中所有点的信息去调整全局状态。
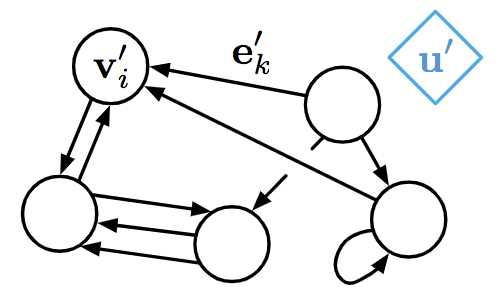
聚合函数需要具有的特点
- 对于参数的顺序不敏感
- 可以接受不定数的变量
举例 : elementwise summation, mean, maximum
图网络中的关系归纳偏置(Relational inductive biases in graph networks)
图网络可表示实体内任意关系,GN’s输入决定实体如何交互和隔离,而非那些固定结构;
图表示实体和关系作为集合,集合排列不变,意味着GN’s对于这些元素顺序不变;
GN的边、节点分别可在所有边和节点上重复使用,GNs自动支持一种组合泛化形式。
Design principles for graph network architectures
一般来说,该框架并不局限属性的表示和函数的形式,在这里,本文更关注深度学习架构,使得GN block 成为一个可学习的 graph-to-graph function approximator。
Flexible representations
GN的灵活性体现在两点:
- 属性值表征的灵活性
- 图的结构本身的灵活性
Attribute
- 属性值的形式
- global, node, edge 的属性可以使用任意的形式表达的. 在深度模型中, 通常是采用real-value vector or tensor 的形式.
输出的单元
根据任务的不同, 输出的东西也是可以不同的. 有三种基本类型的输出.
- edge-focused GN : 采取边作为输出
- node-focused GN : 采取点作为输出, 这个是我们常见的研究
graph-focused GN : 采取global作为输出
还可以有三种的混合形式:
Relational inductive bias for physical construction in humans and machine:
这个研究同时利用edge和global去预测一个(人和机器)基于动作的策略。
Graph structure
有两种场景:
1.输入明确指出了关系结构;
2.必须推断或假设关系结构。
第一个方式的例子:
知识图谱以及句法树以及社会网络问题, 这样的问题中, edge是根据其相连实体来确定的.也就是说, 是基于一个知识图谱或者句法树等等.
第二个方式的例子:
例如, visual scenes, 自然语料库等等. 这样的初始的情况下我们不知道实体之间的任何关系.
具体的例子就是, 将句子中的每一个词汇视为一个node,将图片分 cell,每一个cell 代表一个实体。
Configurable within-block structure
通过对GN进行个性化的定制,我们可以得到不同的网络模型。
Full GN Block
首先是完整的 GN Block:

Non-local neural network
先来简单介绍一下 NLNN:
Non-local neural network在捕捉长距离特征之间依赖关系的基础上提出了一种非局部信息统计的注意力机制。
不管是 CV 任务还是 NLP 任务,都需要捕捉长范围依赖。在时序任务中,RNN 是一种主要的捕获长范围依赖手段,而在 CNN 中是通过堆叠多个卷积块来形成的大感受野。目前的卷积和循环结构都是在空间或者时间上的局部操作,长范围的依赖捕获是通过重复堆叠,并且反向传播得到,会有一些问题:
- 捕获长范围特征依赖需要累计很多层的网络,导致学习效率太低
- 当需要在比较远的位置之间来回传递消息时,卷积或时序局部操作很困难
- 由于网络需要累计很深,需要小心的设计模块和梯度
Local & Non-local
Local 这个词说的是感受野。以卷积操作为例,它的感受野大小就是卷积核大小,只考虑了局部区域, 因此都是 Local 运算。相反,Non-Local 就是值感受野很大,而不仅仅是一个局部区域。
作者提出了一个泛化、简单、可直接嵌入到当前网络的非局部算子,可以捕获时间、空间和时空的长范围依赖。这样设计的好处:
- 相比较于不断堆叠卷积和 RNN 算子,Non-local 直接计算两个位置(可以是时间位置、空间位置和时空位置)之间的关系即可快速捕捉长范围依赖
- Non-local 的计算效率高
- Non-local 可以保证输入尺度和输出尺度不变,这种设计使得 Non-local block 可以很容易嵌入到网络架构中去
Non-local Block
为了能够当作一个组件接入到以前的神经网络中去, Non-local 操作的输入和输出大小一致,具体来说,公式如下:
$$y_i = \frac{1}{C(x)} \sum_{\forall j} f(x_i,x_j)g(x_j)$$
公式中,输入是 x ,可以使图像、序列、视频等,输出是 y。 i 是输出特征图的一个位置,j 是输入所有可能位置索引, f 是相似性计算函数,计算输出中第 i 个位置和其他所有位置的相似性。 g 是一个简单的映射函数,可以看成计算一个点的特征,也就是说,为了计算输出层的一个点,需要将输入的每个点都考虑一遍,而且考虑的方式很像 attention :输出的某个点在原图上的 attention ,而 mask 则是相似性给出。参看下图。

从 GN 的角度来看:

这里的 Entity(Node) 就是公式中的 x,Node的属性就是x的值。
两两 Node 之间包含双向的 Edge(很明显也存在双向的自边)。Edge 的属性是 $(a_k^{‘},b_k^{‘})$。
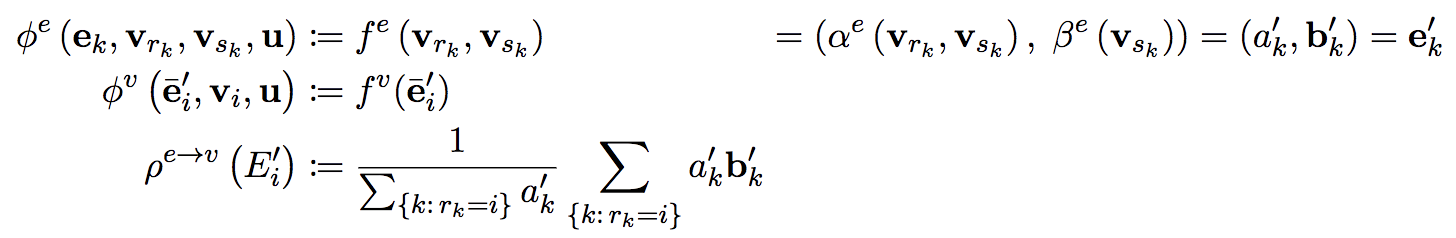
显而易见,这里的 $\alpha^e$ 就是 $f$ 函数,$\beta^e$ 就是 $g$ 函数。
聚合函数 $\rho^{e\rightarrow v}$ 就是 NLNN 的表达式。
Relation Networks
Visual reasoning是个非常重要的问题,由于ResNet等大杀器出现,visual recognition任务本身快要被解决,所以计算机视觉的研究方向逐渐往认知过程的更上游走,即逻辑推理。
下图截取自该论文,可以对 Visual reasoning 又一个更直观的理解:

RN 的网络结构十分简单:
$$RN(O) = f_\phi (\sum_{i,j}g_\theta(o_i, o_j))$$
- Inputs: $O={o_1, …, o_n}$
MLPs: $f_\phi, g_\theta$
$g_\theta$: 使用一个全连接的神经网络来量化 $o_i$ 和 $o_j$ 的关系,任意两个对象之间的关系使用同一套参数 $g_\theta(,)$
$f_\phi (\sum_{i,j}g_\theta(o_i, o_j))$: 考虑所有组合的关系,相当于考虑一个完全连接图,在这个图上计算各个边的权重,把重要的关系凸显出来,f 函数就计算了这个重要关系的集合。
RNs有以下三个特点:
- 可以学习推理。这里 RNs 计算了所有的两个对象之间的关系,当然也可以只计算部分两个对象之间的关系,这里的“部分”需要预定义
- RNs的数据效率更高(data efficient)。RNs 使用一个 g 函数来计算所有的关系,任意两个对象之间的关系使用同一套参数,泛化能力更强
- RNs作用在一个集合上。对输入和输出都是与顺序无关的(input/output invariation)
从 GN 的角度来看:

这里的 Entity(Node) 就是公式中的 o,Node的属性就是 o 的值。
两两 Node 之间包含双向的 Edge(很明显也存在双向的自边),Edge 的属性就是$NN_e$的值。
$NN_e$ 就是 g 函数,$NN_u$ 就是 f 函数。
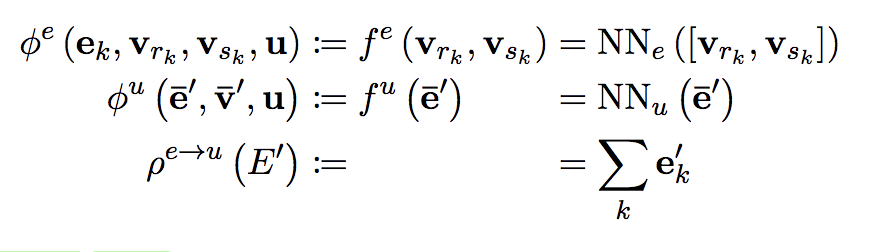
小结
这篇文章给了我们一个抽象的理解深度模型方法的框架,看完之后加深了对很多模型的理解。
Composable multi-block architectures
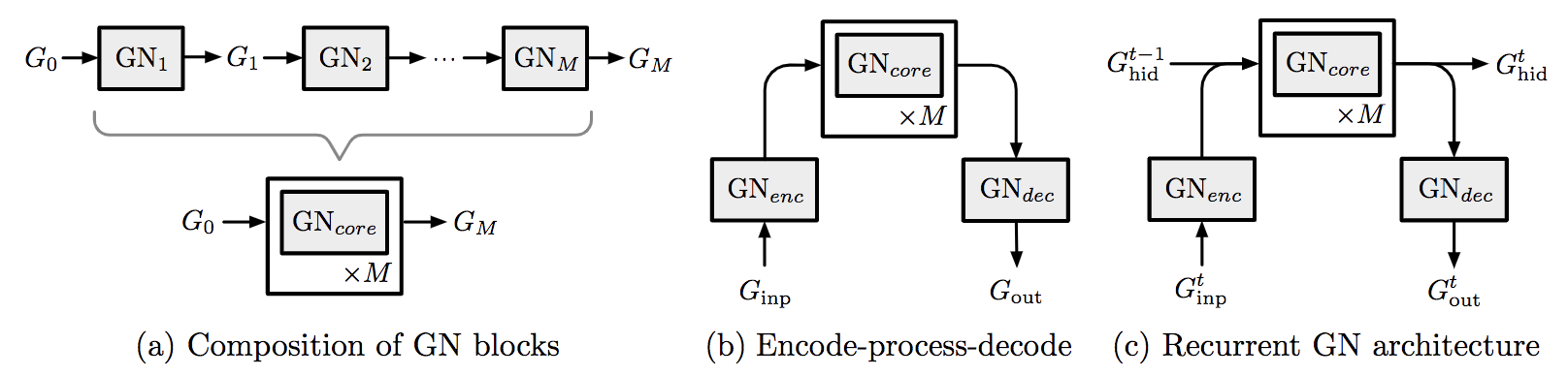
一个GN block的输入和输出都是 graph, 那么一个 Block 的输出就可以当成另外一個 BLock 的输入.即
$$G^{‘} = GN_2(GN_1(G))$$
可以但不限于下面三种组合方式:
总结
私认为,GN 中最为关键的思想就是 Relations。本文将该框架对应于图的神经网络中各种最新的方法进行了归纳和扩展,图网络 GN 被设计为使用可定制的图到图的模块来构建复杂体系结构,它们的关系归纳偏置促进了组合泛化比其它标准机器学习构建块有更高的效率。
