David Silver 强化学习 4 模型无关预测 Model-Free Prediction

2017-10-15

文章目录

1. 简介 Introduction
2. 蒙特卡洛强化学习 Monte-Carlo Reinforcement Learning
3. 时序差分学习 Temporal-Difference Learning
4. Monte-Carlo VS. Temporal Difference
1. 4.1. 确定性等价 Certainty Equivalence
2. 4.2. 三种强化学习算法
5. TD(λ)
6. 小结

简介 Introduction

上节课中通过动态规划能够解决已知 environment 的 MDP 问题，也就是已知 $S,A,P,R,\gamma$，其中根据是否已知 policy 将问题又划分成了 prediction 和 control 问题，本质上来说这种 known MDP 问题已知 environment 即转移矩阵与 reward 函数，但是很多问题中 environment 是未知的，不清楚做出了某个 action 之后会变到哪一个 state 也不知道这个 action 好还是不好，也就是说不清楚 environment 体现的 model 是什么，在这种情况下需要解决的 prediction 和 control 问题就是Model-free prediction和Model-free control。显然这种新的问题只能从与 environment 的交互得到的 experience 中获取信息。

这节课要解决的问题是Model-free prediction，即未知environment的Policy evaluation，在给定的 policy 下，每个state的 value function 是多少。

蒙特卡洛强化学习 Monte-Carlo Reinforcement Learning

蒙特卡洛强化学习是假设每个 state 的 value function 取值等于多个 episodes 的 return Gt 的平均值，它需要每个 episode 是完整的流程，即一定要执行到终止状态。

蒙特卡洛策略评估 Monte-Carlo Policy Evaluation

目标： 在给定策略下，从一系列的完整Episode经历中学习得到该策略下的状态价值函数。

数学描述如下：

基于特定策略 $\pi$ 的一个 Episode信息可以表示为如下的一个序列：
$S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, …, S_{t}, A_{t}, R_{t+1}, …, S_{k}$ ~ $\pi$

t 时刻状态 $S_{t}$ 的收获：
$G_{t} = R_{t+1} + \gamma R_{t+2} + … + \gamma^{T-1} R_{T}$
其中 T 为终止时刻。

该策略下某一状态 s 的价值：
$v_{\pi}(s) = E_{\pi} [ G_{t} | S_{t} = s ]$

在状态转移过程中，可能发生一个状态经过一定的转移后又一次或多次返回该状态，此时在一个Episode里如何计算这个状态发生的次数和计算该Episode的收获呢？可以有如下两种方法：

首次访问蒙特卡洛策略评估

在给定一个策略，使用一系列完整Episode评估某一个状态s时，对于每一个Episode，仅当该状态第一次出现时列入计算:

状态出现的次数加1： $N(s) \leftarrow N(s) + 1$
总的收获值更新： $S(s) \leftarrow S(s) + G_{t}$
状态s的价值： $V(s) = S(s) / N(s)$
当 $N(s) \rightarrow \infty$ 时， $V(s) \rightarrow v_{\pi}(s)$

每次访问蒙特卡洛策略评估

在给定一个策略，使用一系列完整Episode评估某一个状态s时，对于每一个Episode，状态s每次出现在状态转移链时，计算的具体公式与上面的一样，但具体意义不一样。

累进更新平均值 Incremental Mean

这里提到了在实际操作时常用的一个实时更新均值的办法，使得在计算平均收获时不需要存储所有既往收获，而是每得到一次收获，就计算其平均收获。

理论公式如下：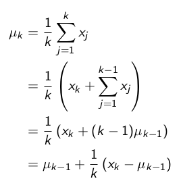
p_1

这个公式比较简单。把这个方法应用于蒙特卡洛策略评估，就得到下面的蒙特卡洛累进更新。

蒙特卡洛累进更新

对于一系列 Episodes 中的每一个： $S_{1}, A_{1}, R_{2}, S_{2}, A_{2}, …, S_{t}, A_{t}, R_{t+1}, …, S_{k} $

对于Episode里的每一个状态 $S_{t}$ ，有一个收获 $G_{t}$ ，每碰到一次 $S_{t}$ ,使用下式计算状态的平均价值 $V(S_{t})$ ：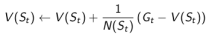
p_2
其中：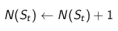
p_3

在处理非静态问题时，使用这个方法跟踪一个实时更新的平均值是非常有用的，可以扔掉那些已经计算过的 Episode 信息。此时可以引入参数 $\alpha$ 来更新状态价值：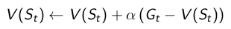
p_4

以上就是蒙特卡洛学习方法的主要思想和描述，由于蒙特卡洛学习方法有许多缺点（后文会细说），因此实际应用并不多。接下来介绍实际常用的TD学习方法。

时序差分学习 Temporal-Difference Learning

时序差分学习简称TD学习，它的特点如下：和蒙特卡洛学习一样，它也从Episode学习，不需要了解模型本身；但是它可以学习不完整的 Episode ，通过自身的引导（bootstrapping），猜测 Episode 的结果，同时持续更新这个猜测。

我们已经学过，在Monte-Carlo学习中，使用实际的收获（return） $G_{t} $来更新价值（Value）：
$V(S_{t}) \leftarrow V(S_{t}) + \alpha (G_{t} - V(S_{t}))$

在 TD 学习中，算法在估计某一个状态的价值时，用的是离开该状态的即刻奖励 $R_{t+1}$ 与下一状态 $S_{t+1}$ 的预估状态价值乘以衰减系数 $\gamma$ 组成，这符合 Bellman 方程的描述：
$V(S_{t}) \leftarrow V(S_{t}) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_{t}))$

式中：
$R_{t+1} + \gamma V(S_{t+1})$ 称为 TD 目标值
$\delta_{t} = R_{t+1} + \gamma V(S_{t+1}) - V(S_{t})$ 称为 TD 误差

BootStrapping 指的就是TD目标值 $R_{t+1} + \gamma V(S_{t+1})$ 代替收获 $G_t$ 的过程，暂时把它翻译成“引导”。

示例——驾车返家

想象一下你下班后开车回家，需要预估整个行程花费的时间。假如一个人在驾车回家的路上突然碰到险情：对面迎来一辆车感觉要和你相撞，严重的话他可能面临死亡威胁，但是最后双方都采取了措施没有实际发生碰撞。如果使用蒙特卡洛学习，路上发生的这一险情可能引发的负向奖励不会被考虑进去，不会影响总的预测耗时；但是在TD学习时，碰到这样的险情，这个人会立即更新这个状态的价值，随后会发现这比之前的状态要糟糕，会立即考虑决策降低速度赢得时间，也就是说你不必像蒙特卡洛学习那样直到他死亡后才更新状态价值，那种情况下也无法更新状态价值。

TD算法相当于在整个返家的过程中（一个Episode），根据已经消耗的时间和预期还需要的时间来不断更新最终回家需要消耗的时间。

p_5

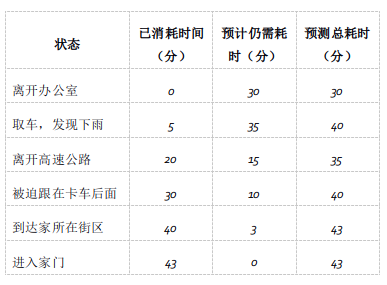
基于上表所示的数据，下图展示了蒙特卡洛学习和TD学习两种不同的学习策略来更新价值函数（各个状态的价值）。这里使用的是从某个状态预估的到家还需耗时来间接反映某状态的价值：某位置预估的到家时间越长，该位置价值越低，在优化决策时需要避免进入该状态。对于蒙特卡洛学习过程，驾驶员在路面上碰到各种情况时，他不会更新对于回家的预估时间，等他回到家得到了真实回家耗时后，他会重新估计在返家的路上着每一个主要节点状态到家的时间，在下一次返家的时候用新估计的时间来帮助决策；而对于TD学习，在一开始离开办公室的时候你可能会预估总耗时30分钟，但是当你取到车发现下雨的时候，你会立刻想到原来的预计过于乐观，因为既往的经验告诉你下雨会延长你的返家总时间，此时你会更新目前的状态价值估计，从原来的30分钟提高到40分钟。同样当你驾车离开高速公路时，会一路根据当前的状态（位置、路况等）对应的预估返家剩余时间，直到返回家门得到实际的返家总耗时。这一过程中，你会根据状态的变化实时更新该状态的价值。

p_6

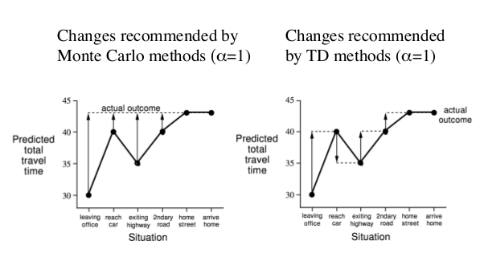
Monte-Carlo VS. Temporal Difference

在谈两种算法的优劣前，先谈谈 Bias/Variance tradeoff 的问题。平衡 Bias/Variance 是机器学习比较经典的一个问题，bias 是指预测结果与真实结果的差值，variance 是指训练集每次预测结果之间的差值，bias 过大会导致欠拟合它衡量了模型是否准确，variance 过大会导致过拟合衡量了模型是否稳定。如果 $G_t$ 和 $R_{t+1} + \gamma v_{\pi} (S_{t+1})$ 跟真实值一样，那么就是无偏差估计。因为在MC算法中，它是将最终获得的 reward 返回到了前面的状态，因此是真实值，但是它采样的 episode 并不能代表所有的情况，所以会导致比较大的 variance 。而 TD的 $R_{t+1} + \gamma v_{\pi} (S_{t+1})$ 跟真实值是有偏差的，在计算的过程基于随机的状态、转移概率、reward 等等，涵盖了一些随机的采样，因此 variance 比较小。

示例——AB
已知：现有两个状态(A和B)，MDP未知，衰减系数为1，有如下表所示8个完整Episode的经验及对应的即时奖励，其中除了第1个Episode有状态转移外，其余7个均只有一个状态。

p_8

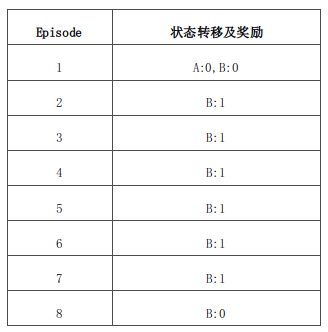
问题：依据仅有的Episode，计算状态A，B的价值分别是多少，即V(A)=？， V(B)=？

答案：V(B) = 6/8，V(A)根据不同算法结果不同，用MC算法结果为0，TD则得出6/8。

解释：应用MC算法，由于需要完整的 Episode ,因此仅 Episode1 可以用来计算A的状态价值，很明显是0；同时B的价值是6/8。应用 TD 算法时，TD 算法试图利用现有的 Episode 经验构建一个 MDP（如下图），由于存在一个 Episode 使得状态A有后继状态 B ，因此状态A的价值是通过状态B的价值来计算的，同时经验表明 A 到 B 的转移概率是100%，且A状态的即时奖励是0，并且没有衰减，因此A的状态价值等于 B 的状态价值。

p_9

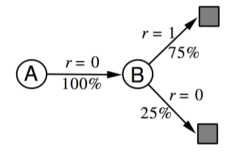
确定性等价 Certainty Equivalence

MC算法试图收敛至一个能够最小化状态价值与实际收获的均方差的解决方案，这一均方差用公式表示为：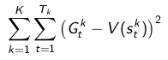
p_10

式中，k 表示的是 Episode 序号， K 为总的 Episode 数量， t 为一个 Episode 内状态序号（第1,2,3…个状态等）， $T_{k}$ 表示的是第 k 个Episode总的状态数， $G^{k}_{t}$ 表示第 k 个 Episode 里 t 时刻状态 $S_{t}$ 获得的最终收获， $V(S^{k}_{t})$ 表示的是第 k 个 Episode 里算法估计的 t 时刻状态 $S_{t}$ 的价值。

TD算法则收敛至一个根据已有经验构建的最大可能的马儿可夫模型的状态价值，也就是说TD算法将首先根据已有经验估计状态间的转移概率：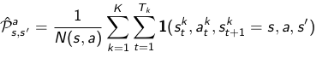
p_11

同时估计某一个状态的即时奖励：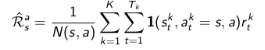
p_12

最后计算该MDP的状态函数。

三种强化学习算法

Monte-Carlo, Temporal-Difference 和 Dynamic Programming 都是计算状态价值的一种方法，区别在于，前两种是在不知道Model的情况下的常用方法，这其中又以MC方法需要一个完整的Episode来更新状态价值，TD则不需要完整的Episode；DP方法则是基于Model（知道模型的运作方式）的计算状态价值的方法，它通过计算一个状态S所有可能的转移状态S’及其转移概率以及对应的即时奖励来计算这个状态S的价值。

关于是否采用 Bootstrap： MC 没有引导数据，只使用实际收获；DP和TD都有引导数据。
关于是否用采样 Sampling: MC和TD都是应用样本来估计实际的价值函数；而DP则是利用模型直接计算得到实际价值函数，没有样本或采样之说。

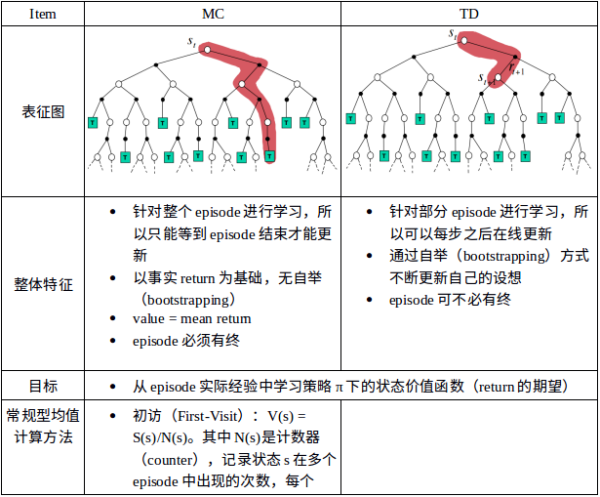
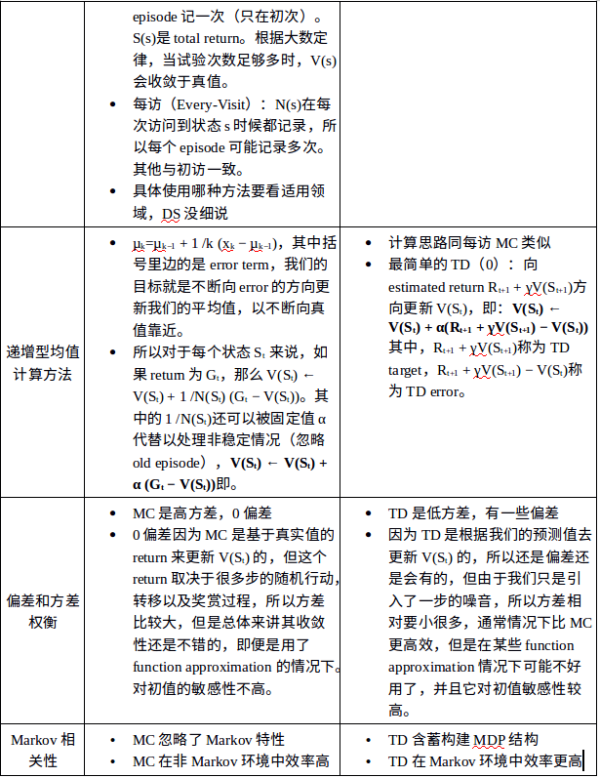
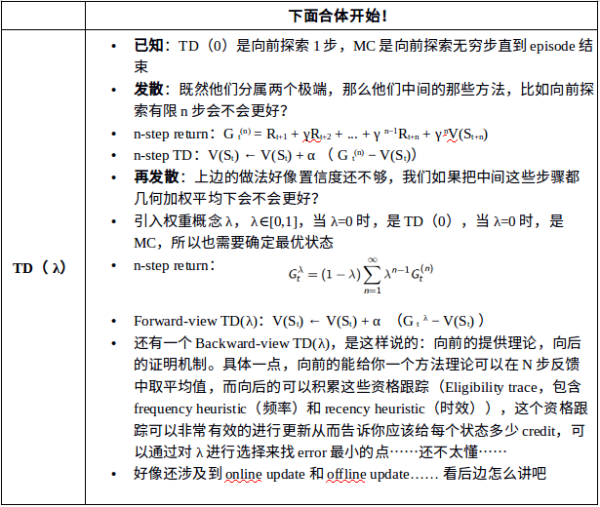
下面的几张图直观地体现了三种算法的区别：

p_13

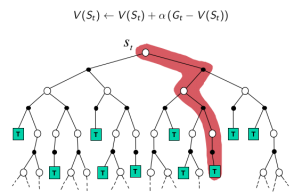
MC: 采样，一次完整经历，用实际收获更新状态预估价值

p_14

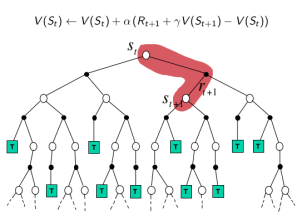
TD：采样，经历可不完整，用喜爱状态的预估状态价值预估收获再更新预估价值

p_15
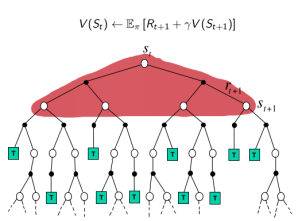
DP：没有采样，根据完整模型，依靠预估数据更新状态价值

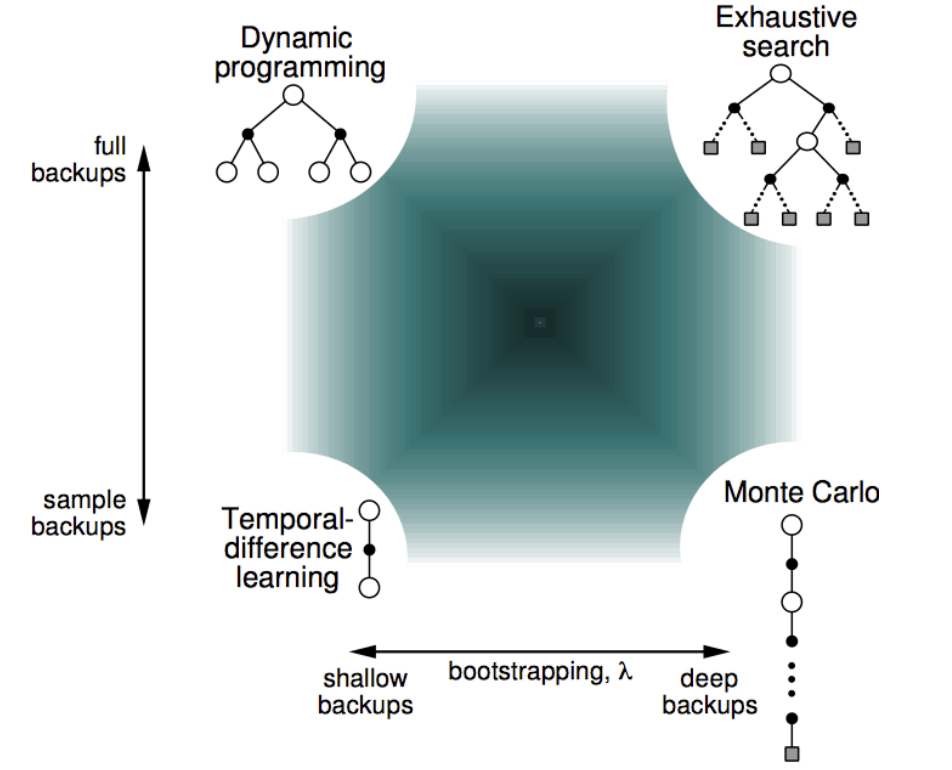
上图从两个维度解释了四种算法的差别，多了一个穷举法。
这两个维度分别是：采样深度和广度。

当使用单个采样，同时不走完整个Episode就是TD；
当使用单个采样但走完整个Episode就是MC；
当考虑全部样本可能性，但对每一个样本并不走完整个Episode时，就是DP；
当既考虑所有Episode又把Episode从开始到终止遍历完，就变成了穷举法。

需要提及的是：DP利用的是整个MDP问题的模型，也就是状态转移概率，虽然它并不实际利用样本，但是它利用了整个模型的规律，因此认为是Full Width的。

TD(λ)

TD(0) 是指在某个状态 s 下执行某个动作后转移到下一个状态 s′ 时，估计 s′ 的 return 再更新 s ，假如 s 之后执行两次动作转移到 s″ 时再反回来更新s的值函数，那么就是另一种形式，从而根据 step 的长度 n 可以扩展 TD 到不同的形式，当 step 长度到达当前 episode 终点时就变成了 MC。

定义 n-step 收获：
$G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + … + \gamma ^{n-1}R_{t+n}+\gamma ^nV(S_{t+n})$

n = 1 时即 TD(0)

那么，n-step TD 学习状态价值函数的更新公式为：
$V(S_t) \leftarrow V(S_t) + \alpha(G_t^{(n)} - V(S_t))$

既然存在 n-step 预测，那么n=？时效果最好呢?

前向认知 TD(λ) The Forward View of TD(λ)

如果将不同的 n 对应的 $G_t^{(n)}$ 平均一下，这样能够获得更加 robust 的结果，而为了有效的将不同 $G_t^{(n)}$ 结合起来，对每个 n 的 $G_t^{(n)}$ 都赋了一个权重 $1-\lambda,(1-\lambda)\lambda,…,(1-\lambda)\lambda^{n-1},\lambda^{T-t-1}$ ，T 是状态的总数, t 表示了在第几个状态，所有的权重加起来为1,这样又能得到一组更新 value function 的公式。

$G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{\infty }\lambda^{n-1}G_t^{(n)}$
为了更好的把episode的terminal state体现出来，我们可以写成下式：
$G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{T-t-1 }\lambda^{n-1}G_t^{(n)} + \lambda^{T-t-1}G_t^{(T-t)}$

$V(S_t) \leftarrow V(S_t) + \alpha(G_t^{\lambda} - V(S_t))$

下图是各步收获的权重分配图

p_17

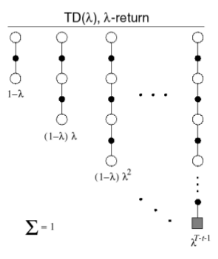
对于每个访问到的state，我们都是从它开始向前看所有的未来reward，并决定如何结合这些reward来更新当前的state。每次我们更新完当前state，我们就到下一个state，永不再回头关心前面的state。这种感觉就像下图一样：

p_26

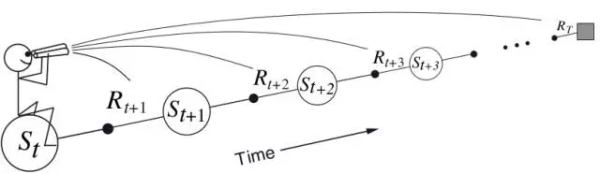
TD(λ)对于权重分配的图解

p_18

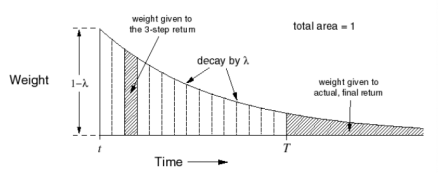
对于 n=3 的 3-步收获，赋予其在 $\lambda$ 收获中的权重如左侧阴影部分面积，对于终止状态的 T-步收获，T以后的所有阴影部分面积。而所有节段面积之和为1。这种几何级数的设计也考虑了算法实现的计算方便性。

在实际任务中这类算法却很少用，因为不便于实现：在n-step TD中，你需要等待 n 步之后观测得到的reward和state。如果n很大，这个等待过程就是个问题，存在很大的滞后性，这是一个待解决问题。那么n-step TD有什么意义呢？n-step TD的思想可以让我们更好理解接下来的”资格迹“方法。

后向认知 TD(λ) The Backward View of TD(λ)

TD(λ)的后向视角非常有意义，因为它在概念上和计算上都是可行而且简单的。具体来说，前向视角只提供了一个非常好但却无法直接实现的思路，因为它在每一个timestep都需要用到很多步之后的信息，这在工程上很不高效。而后向视角恰恰解决了这个问题，采用一种带有明确因果性的递增机制来实现TD(λ)，最终的效果是在on-line case和前向视角近似，在off-line case和前向视角精确一致。

后向视角的实现过程中，引入了一个额外的和每个state都相关的存储变量，它的名字就叫做“资格迹”。在t时刻的状态s对应的资格迹，标记为 $Z_t(s) \in \mathbb{R}^+$ 。资格迹的更新方式如下：

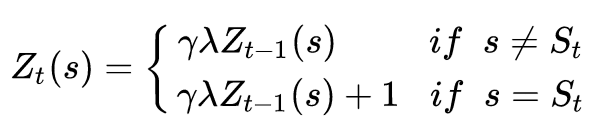
稍微解释一下上面式子的含义：在一开始，每个episode中的所有状态都有一个初始资格迹，然后时间开始走。到下一个timestep，被访问到的那个状态，其资格迹为前一个时刻该状态资格迹乘上一个（decay param 乘 discount param），然后加1，表示当前时刻，该状态的资格迹变大；其他未被访问的状态，其资格迹都只是在原有基础上乘以（decay param*discount param），不用加1,表明它们的资格迹都退化了。

我们把λ成为“迹退化参数”，把上式这种更新方式的资格迹叫做“累加型资格迹”。因为它在状态被访问的时候累加，不被访问的时候退化。如下图：

p_19

常规的TD误差如下式：
$\delta_t = R_{t+1} + \gamma V_t(S_{t+1})-V_t(S_t)$

但是在TD(λ)的后向视角中，这个误差却可以影响所有“最近”访问过的状态的，对于这些状态来说，TD误差如下：
$\Delta V_t(s) = \alpha \delta_tZ_t(s) \;\;for \; all \; s\in S$

可以这么说：后向视角的TD(λ)，才是真正的TD(λ)。我们来更形象地表述一下后向视角的过程：每次在当前访问的状态得到一个误差量的时候，这个误差量都会根据之前每个状态的资格迹来分配当前误差。这就像是一个小人，拿着当前的误差，然后对准前面的状态们按比例扔回去，就像下图一样：

p_20

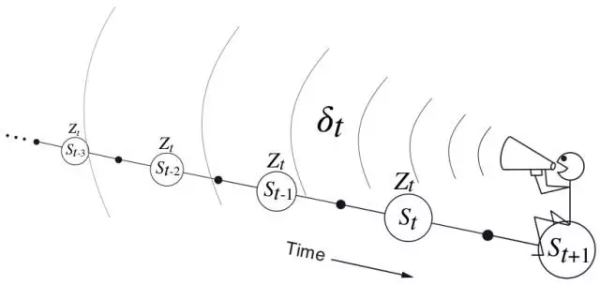
λ=0:TD(λ)退化成TD(0)，除了当前状态，其他所有状态的资格迹为0。这时候，小人不再向前面扔误差量，而是只给当前状态了。随着λ变大，但是小于1,更多状态的误差被当前误差所影响，越远的，影响越小。我们称越远的状态被分配的credit（可以理解为信用）越少。

λ=1:当 $\gamma$ 不等于1时， $\delta_t$ 依照 $\gamma^k$ 逐步递减；如果 $\gamma$ 等于1，那么资格迹就不再递减。我们把λ=1时的TD算法也叫做TD(1)。

传统MC如果不走到episode结束，是什么都学不到的。而且传统MC只适用于非连续式，有明确终点状态的任务。再看TD(1)，读者可以把它想象成拖着一条移动的长尾巴的MC类算法（你可以把传统MC看成是有一条固定的长尾巴算法），可以即时地从正在进行的episode中学习，基于它的控制方法可以及时地修正后续episode的生成方式。因此TD(1)不仅适用于片段式任务，也适用于连续性任务。

Equivalence of Forward and Backward Views

参考：https://zhuanlan.zhihu.com/p/27773020

小结

下表给出了λ取各种值时，不同算法在不同情况下的关系。

p_21

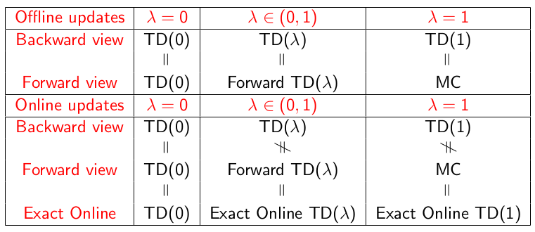
内容的图标总结：

p_22

p_23

p_24