从Fictitious Play 到 NFSP

2017-07-27

文章目录

1. 博弈论
2. FSP in Extensive-Form Games
1. 2.1. Extensive-Form 定义扩充
2. 2.2. Normal-Form 定义扩充
3. Fictitious Play
4. Realization-equivalence
5. Extensive-Form Fictitious Play
6. Fictitious Self-Play
7. Neural Fictitious Self-Play
8. REF：

博弈论

Normal-form game

在博弈论中，Normal-form game是对game的一种描述。Normal-form game通过矩阵来表示game。
下图就是一个payoff矩阵：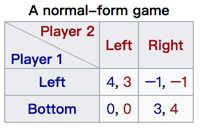
payoff
Normal-form game是一种静态模型，这个模型假设每个player仅选择一次action或策略。
Normal-form game适用于描述不需要考虑博弈进程的完全信息静态(Complete information static)博弈。

静态博弈
players同时进行决策
动态博弈
players的决策顺序有先后
完全信息(Complete information)
在完全信息博弈中，players的游戏结构和players的payoff矩阵是众所周知的，但players可能看不到其他players所做的所有动作。
完美信息(Perfect information)
在完美信息博弈中，每个player可以观测到其他players的动作，但可能缺乏关于他人的payoff或游戏结构的信息。

Extensive-form game

Extensive-form game是一种动态模型。通过使用树这种图形来表示game。不仅给出了博弈结果，还描述了博弈过程，如给出博弈中参与人的行动顺序，以及决策环境和行动空间等。
完美信息下的Extensive-form game: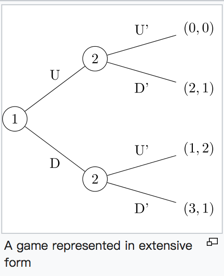

If player 1 plays D, player 2 will play U’ to maximise his payoff and so player 1 will only receive 1. However, if player 1 plays U, player 2 maximises his payoff by playing D’ and player 1 receives 2. Player 1 prefers 2 to 1 and so will play U and player 2 will play D’

非完美信息下的Extensive-form game:

信息集 是一组决策节点：

集合中的每个节点都只属于一个player；
当player到达信息集时，player不能区分信息集中的节点。即，如果信息集包含多个节点，则该集合所属的player不知道集合中的哪个节点已经到达。

下图的虚线连接的两个节点2代表player2的一个信息集，player2不知道player1采取的是U还是D。
补充：在扑克游戏中，player不知道的是对方的手牌信息而不是这个例子中的动作。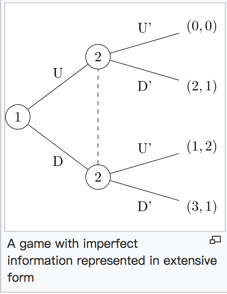

player 2 cannot observe player 1’s move. Player 1 would like to fool player 2 into thinking he has played U when he has actually played D so that player 2 will play D’ and player 1 will receive 3.

ref : https://en.wikipedia.org/wiki/Extensive-form_game

Extensive-form game和Normal-form game的转换

下图是Extensive-form game的一个例子：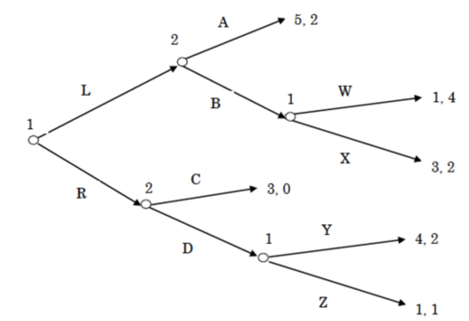

player1有三个信息集，每个信息集里面有两种行动，所以player1有8种策略；player2有两个信息集，每个信息集里面有两种行动，所以player2有4种策略。
所以转换成Normal-form game是一个横8纵4的矩阵.

FSP in Extensive-Form Games

Extensive-Form 定义扩充

Chance
Chance被认为是一个特别的player，遵循一个固定的随机策略，决定了chance节点进入每个分支的概率分布。（如扑克游戏中的发牌）。
Information State
我们假设游戏具有perfect recall，即每个player当前的信息状态u隐含了之前的信息状态和行动序列: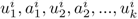
Behavioural Strategy
在给定Information State时，动作action的概率分布。Behavioural Strategy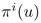 输出player i在信息状态u下，动作的概率分布。
Normal-Form 定义扩充
Pure Strategy
player在可能遇到的所有情况下都有一个确定的动作action。(payoff矩阵中的每一行和列都是一个Pure Strategy)
Mixed Strategy
Mixed Strateg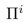是Player i的Pure Strategy的概率分布。

Fictitious Play

!图20
在normal form下：
当前策略 = 现有策略和bestResponse的加权平均。

Realization-equivalence

也就是说，Extensive-Form下的Behavioural Strategy和Normal-form下的Mixed Strategy存在一种等价。
Extensive-Form也可以使用Normal-form下的Fictitious Play来求纳什均衡解。

Extensive-Form Fictitious Play

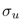图12 代表到信息状态u的sequence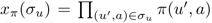
图11
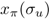图13 = sequence 中每个节点选择每个action的概率乘积

下图是对Lemma 6的一个计算的验证。
图14
图10

我们通过Theorem7更新Behavioural Strategy，可以收敛到纳什均衡。

具体算法XFP：
图15

计算bestResponse
更新策略，使用Theorem7

重复上面的过程

Fictitious Self-Play

XFP会有维度灾难。generalised weakened fictitious play只需要近似bestResponse，甚至允许更新中的一些扰动。

Fictitious Self-Play：

使用强化学习去计算bestResponse
使用监督学习更新策略

图16
样本的采集 GENERATEDAT()方法需要在理解一下。

Neural Fictitious Self-Play

强化学习和监督学习都使用神经网络去学习出一个函数。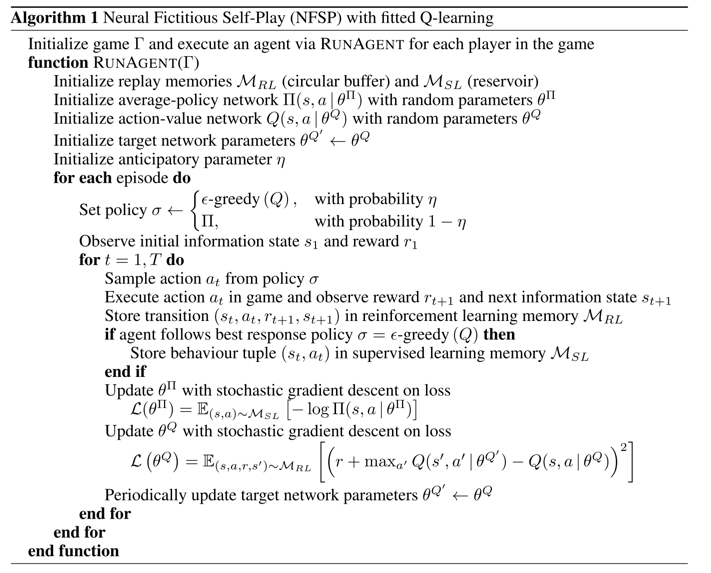
图17

FSP中样本采集的混合策略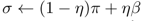图18 ，在NSFP中是函数，不能简单相加。
转换成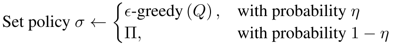图19 ，使用概率完成上面式子中的加操作。

REF：

Topics in Algorithmic Game Theory February 8, 2010 Lecturer: Constantinos Daskalakis Lecture 2
Fictitious Self-Play in Extensive-Form Games
Deep Reinforcement Learning from Self-play in imperfect-information games

博弈论